DEFINICIÓN DEVALOR ABSOLUTO

La noción de valor absoluto se utiliza en el terreno de las matemáticas para nombrar al valor que tiene un número más allá de su signo. Esto quiere decir que el valor absoluto, que también se conoce como módulo, es la magnitud numérica de la cifra sin importar si su signo es positivo o negativo.

Tomemos el caso del valor absoluto 5. Este es el valor absoluto tanto de +5 (5 positivo) como de -5 (5 negativo). El valor absoluto, en definitiva, es el mismo en el número positivo y en el número negativo: en este caso, 5. Cabe destacar que el valor absoluto se escribe entre dos barras verticales paralelas; por lo tanto, la notación correcta es |5|.

La definición del concepto indica que el valor absoluto siempre es igual o mayor que 0 y nunca es negativo. Por lo dicho anteriormente, podemos agregar que el valor absoluto de los números opuestos es el mismo. 8 y -8, de este modo, comparten el mismo valor absoluto: |8|.

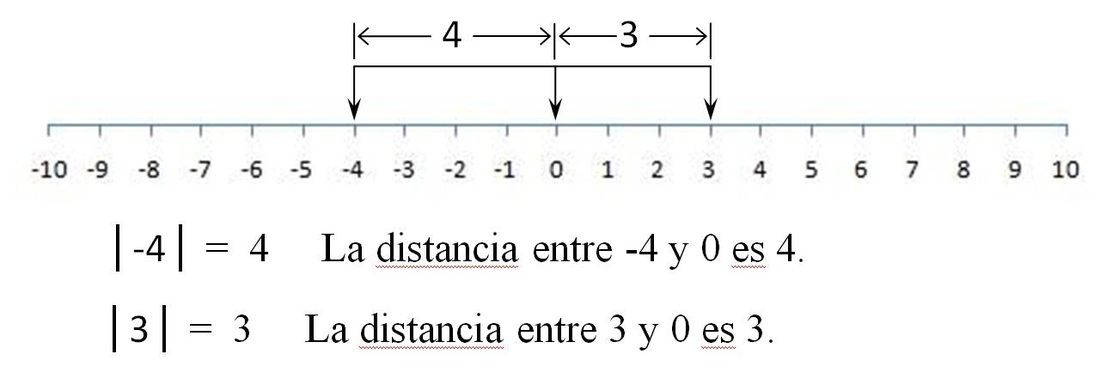
También se puede entender al valor absoluto como la distancia que existe entre el número y 0. El número 563 y el número -563 están, en una recta numérica, a la misma distancia del 0. Ese, por lo tanto, es el valor absoluto de ambos: |563|.

La distancia que existe entre dos números reales, por otra parte, es el valor absoluto de su diferencia. Entre 8 y 5, por ejemplo, hay una distancia de 3. Esta diferencia tiene un valor absoluto de |3|.

Las funciones en valor absoluto se transforman en funciones a trozos, siguiendo los siguientes pasos:Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces.Se forman intervalos con las raíces y se evalúa el signo de cada intervalo.Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función.